Plotting a Lissajous curve

We can determine the points of a Lissajous curve with the lissajous function. The function returns a data frame with values of x and y, and ratio and phase variables are added for later plots

lissajous <- function(w1, w2, diff_phase, ratio, phase){
  t <- seq(0, 2*pi, length.out = 100)
  x <- sin(w1*t + diff_phase)
  y <- sin(w2*t)
  df <- data.frame(x = x, y = y, ratio = ratio, phase = phase)
  return(df)
}

Once we have the coordinates of the plots, we can represent the curve with geom_path(). This geom connects observations in the order they appear in the data. If we use geom_line() points are connected by order of the x axis. I use theme_void() because I don’t need coordinate axis in this kind of plots.

ggplot(lissajous(w1 = 1, w2 = 3, diff_phase = pi/4, ratio = "1/3", phase = "pi/4"), aes(x,y)) +
  geom_path() +
  theme_void()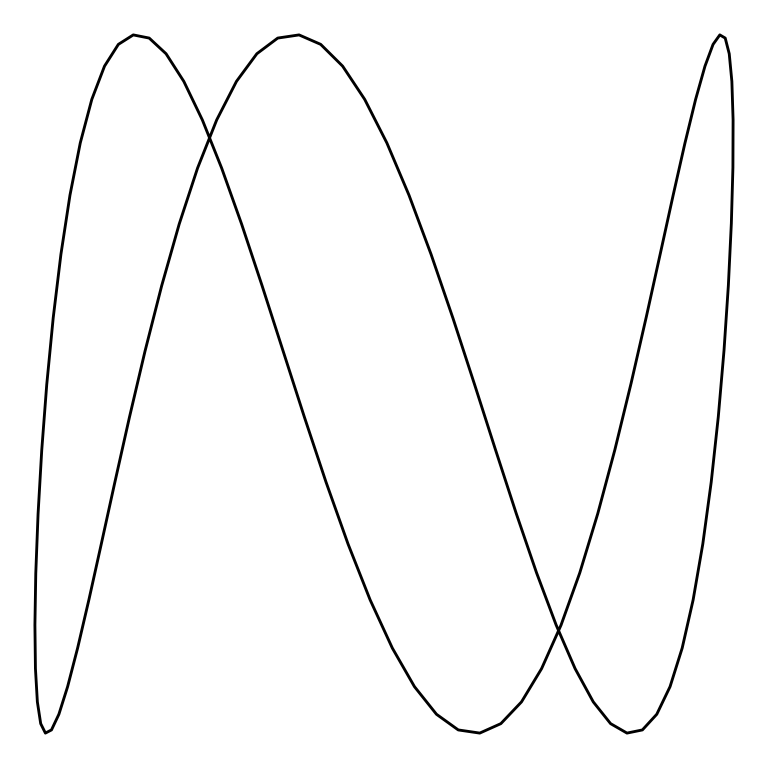 

The above plot is a Lissajous curve with \(w_1=1\) and \(w_2=3\). Note that the figure has one vertical lobe and three horizontal lobes.

Plotting several Lissajous curves at once

Let’s try to plot several Lissajous curves together. I will be plotting eight ratios of frequencies for five different phase differences. I am using expand.grid for generating all combinations and mutate to obtain function parameters from ratio and phase labels.

lissajous_values <- expand.grid(ratio = c("1/1", "1/2", "1/3", "2/3", "3/4", "3/5", "4/5", "5/6"), phase = c("0", "pi/4", "pi/2", "3pi/4", "pi"))

lissajous_values <- lissajous_values %>%
  mutate(w1 = as.numeric(substr(ratio, 1, 1)),
         w2 =  as.numeric(substr(ratio, 3, 3)),
         phase_num = case_when(phase == "0" ~ 0,
                               phase == "pi/4" ~ pi/4,
                               phase == "pi/2" ~ pi/2,
                               phase == "3pi/4" ~ 3*pi/4,
                               phase == "pi" ~ pi))

Let’s glimpse at the table:

lissajous_values %>% glimpse()

## Rows: 40
## Columns: 5
## $ ratio     <fct> 1/1, 1/2, 1/3, 2/3, 3/4, 3/5, 4/5, 5/6, 1/1, 1/2, 1/3, 2/3, …
## $ phase     <fct> 0, 0, 0, 0, 0, 0, 0, 0, pi/4, pi/4, pi/4, pi/4, pi/4, pi/4, …
## $ w1        <dbl> 1, 1, 1, 2, 3, 3, 4, 5, 1, 1, 1, 2, 3, 3, 4, 5, 1, 1, 1, 2, …
## $ w2        <dbl> 1, 2, 3, 3, 4, 5, 5, 6, 1, 2, 3, 3, 4, 5, 5, 6, 1, 2, 3, 3, …
## $ phase_num <dbl> 0.0000000, 0.0000000, 0.0000000, 0.0000000, 0.0000000, 0.000…

Now we need to apply the lissajous function to each row of the table, and integrate the resulting 40 data frames of 100 rows into a single data frame. We can do that using the pmap_df function of the purrr package:

lissajous_table <- pmap_df(lissajous_values, function(ratio, phase, w1, w2, phase_num) lissajous(w1 = w1, w2 = w2, diff_phase = phase_num, ratio = ratio, phase = phase))

The resulting data frame lissajous_table has 40 x 100 = 4,000 rows:

lissajous_table %>% glimpse()

## Rows: 4,000
## Columns: 4
## $ x     <dbl> 0.00000000, 0.06342392, 0.12659245, 0.18925124, 0.25114799, 0.31…
## $ y     <dbl> 0.00000000, 0.06342392, 0.12659245, 0.18925124, 0.25114799, 0.31…
## $ ratio <fct> 1/1, 1/1, 1/1, 1/1, 1/1, 1/1, 1/1, 1/1, 1/1, 1/1, 1/1, 1/1, 1/1,…
## $ phase <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…

To plot the forty Lissajous curves we use a single plot:

• x and y as aesthetics of each plot, created with geom_path() and theme_void().
• we use ratio and phase as arguments of facet_grid() (that’s why they are added to the lissajous function). The switch = "y" argument sets the labels of frequency ratio to the left instead of to the right.

ggplot(lissajous_table, aes(x,y)) +
  geom_path() + 
  theme_void() +
  facet_grid(ratio ~ phase, switch = "y")

Examining the effect of phase with an animated GIF

To finish this gallery of Lissajous plots I have shown the effect of phase difference for a Lissajous curve. To run this on your computer you need:

• the gganimate package to create the plots to be wrapped into the animation,
• the transformr package to generate smooth transitions between contiguous plots of the animation
• and the gifski package to create the GIF.

The code to build the GIF is wrapped into the lissajous_gif function:

• The values data frame has points values of diff_phase between 0 and \(2\pi\). We will be using 100 images to build the GIF, one for each value of phase difference.
• The l_gif function returns the points of a Lissajous curve for each diff_phase using a number of points. These values are stored in the table data frame.
• I use the transition_states function of gganimate to generate the plots to build the GIF. The function will generate one plot for each value of diff_phase.
• The function returns the set of plots of the anim variable.

lissajous_gif <- function(w1, w2, points = 100){
  
  values <- data.frame(w1, w2, diff_phase = seq(0, 2*pi, length.out = 100))
  
  l_gif <- function(w1, w2, diff_phase){
    t <- seq(0, 2*pi, length.out = points)
    x <- sin(w1*t + diff_phase)
    y <- sin(w2*t)
    df <- data.frame(x = x, y = y, diff_phase = diff_phase)
    return(df)
  }
  
  table <- pmap_df(values, function(w1, w2, diff_phase) l_gif(w1, w2, diff_phase))
  
  anim <- ggplot(table, aes(x, y)) +
    geom_path() +
    theme_void() +
    transition_states(diff_phase,
                      transition_length = 2,
                      state_length = 1)
  
  return(anim)
}

Let’s see an animation for a Lissajous curve of \(w_1 = 2\) and “w_2 = 3”

lissajous_gif(w1=2, w2=3, points=100)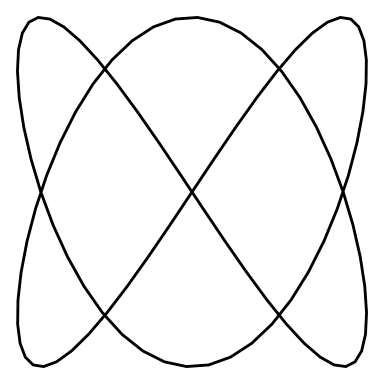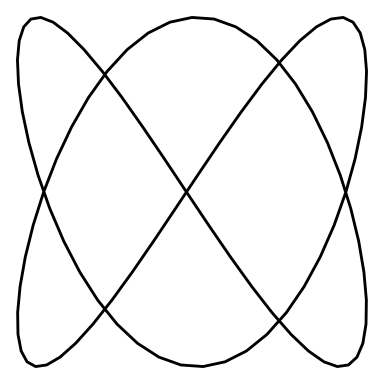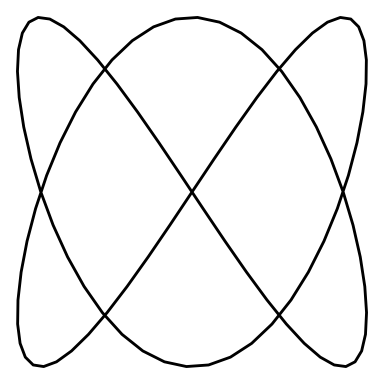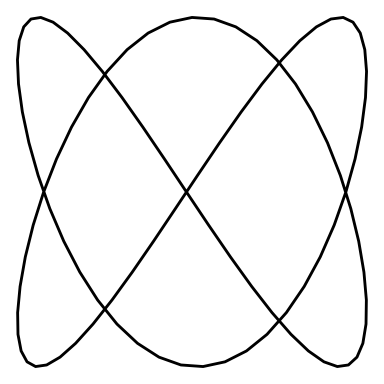

And an animation for \(w_1 = 4\) and \(w_2 = 5\):

lissajous_gif(w1=4, w2=5, points=500)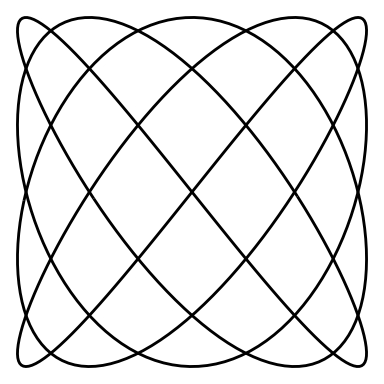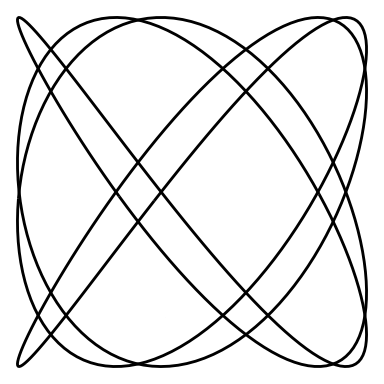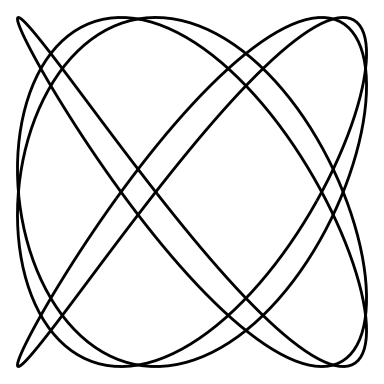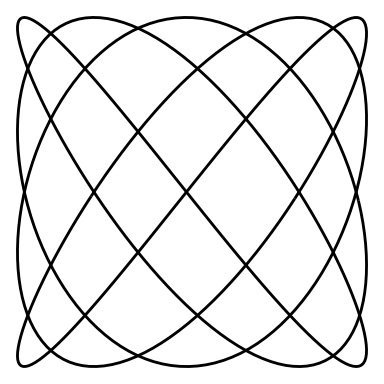

Built with R 4.1.0, dplyr 1.0.7, gganimate 1.0.7, ggplot2 3.3.4, purrr 0.3.4, and transformr 0.1.3